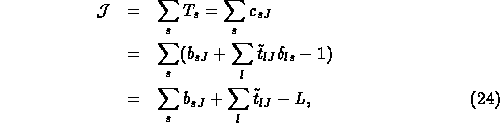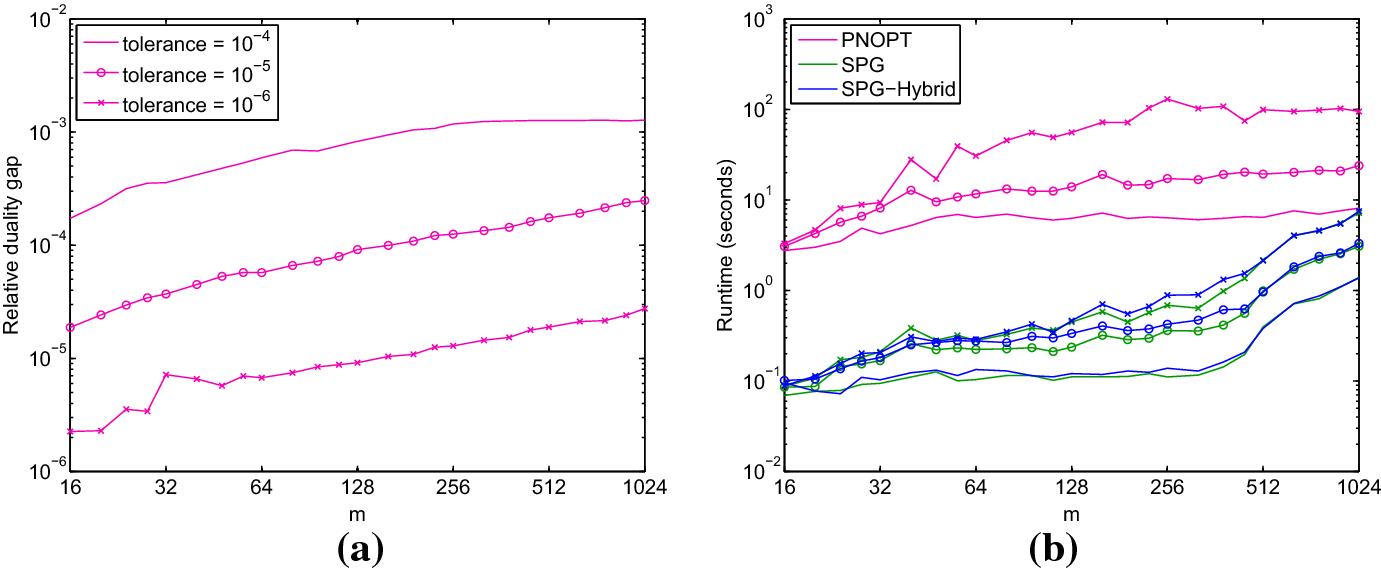
Figure 4 | A hybrid quasi-Newton projected-gradient method with application to Lasso and basis-pursuit denoising | SpringerLink
A note on the duality gap in nonconvex optimization and a very simple procedure for bid evaluation type prob|ems

Characterizations of ɛ-duality gap statements for constrained optimization problems – topic of research paper in Mathematics. Download scholarly article PDF and read for free on CyberLeninka open science hub.
Chapter 3: Convexity Chapter 4: Primal optimality conditions Chapter 5: Primal–dual optimality conditions Chapter 6: Lagrangia

Fig. A0.2. An example of duality gap arising from non-convexity (see text). | Download Scientific Diagram
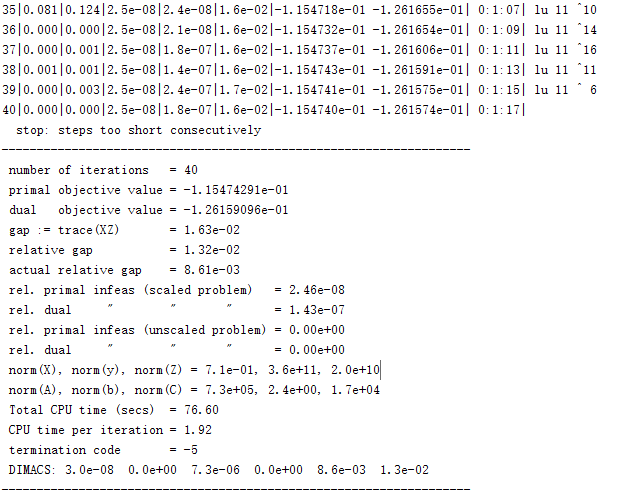


![PDF] DUALITY GAP ESTIMATION VIA A REFINED | Semantic Scholar PDF] DUALITY GAP ESTIMATION VIA A REFINED | Semantic Scholar](https://d3i71xaburhd42.cloudfront.net/e0c09c654e2e5316fb581a5a6ca48a3cdd1fec1b/16-Figure2-1.png)